Специфические вопросы оценки эффективности проектов коммерческой недвижимости
Болотин С.А., Лемешко Д.С.
Болотин Сергей Алексеевич - заведующий кафедрой Экспертизы и управления недвижимостью Санкт-Петербургского государственного архитектурно-строительного университета (СПбГАСУ), доктор технических наук, профессор. Специалист в области организации строительства. Ведет курс "Организация строительства и управление недвижимостью". Автор более 100 научных трудов.
Лемешко Дмитрий Сергеевич - управляющей проектом развития сети ООО "ХКФ-банк", аспирант Санкт-Петербургского государственного архитектурно-строительного университета (СПбГАСУ).
На неоднозначность традиционных методов оценки эффективности инвестиционных проектов с длительными сроками планирования обращают внимание в своей статье д.т.н., проф. СПбГАСУ С.А.Болотин и специалист ООО "ХКФ-банк" Д.С.Лемешко. Они предлагают дополнить эти методы новыми критериями оценки, опираясь на математический материал и графические построения зависимостей чистого дисконтированного потока от нормы дисконта.
В последнее время в России интенсивно развивается рынок коммерческой недвижимости: возводятся новые торгово-развлекательные центры, логистические терминалы, высококлассные бизнес-центры и другие аналогичные объекты. На стадии анализа наиболее эффективного использования объектов недвижимости коммерческого класса ключевыми инвестиционными показателями традиционно выступают чистый дисконтированный доход (NPV) и внутренняя норма рентабельности (IRR), одним из определяющих параметров которых является продолжительность денежного потока. Тенденция переходного периода развития российской экономики состоит в том, что происходит естественный переход от краткосрочного к среднесрочному инвестированию. Поэтому сейчас довольно часто российского девелопера интересует двухлетний горизонт планирования, обычно включающий один инвестиционный год и один год возврата вложенных денежных средств. В странах с более развитой рыночной экономикой расчет эффективности проекта ориентирован на больший период, связанный со средним сроком жизни объекта. Например, жизненный цикл крупного торгового центра составляет в среднем от 5 до 10 лет, после чего полностью меняется концепция использования этого объекта. Для логистических комплексов потребность в реновации может возникнуть еще раньше, через 4-7 лет. На наш взгляд, этих примеров достаточно для вывода о том, что в дальнейшем и в России эффективность коммерческих проектов будет учитывать все больший горизонт планирования.
Рассмотрим характерный тип объектов коммерческой недвижимости, а именно логистические терминалы, обладающие краткосрочным жизненным циклом. В настоящее время в Санкт-Петербурге большинство складских комплексов - это перепрофилированные территории и здания промышленных предприятий. Редевелопмент подобных объектов является дорогостоящим мероприятием, требующим привлечения значительных денежных и людских ресурсов, так как подобные здания и сами территории далеки по своим характеристикам от вновь созданных логистических комплексов с точки зрения транспортных схем организации движения, оснащенности грузоподъемными механизмами, планировочных решений складских корпусов (несоответствие высоты потолков, длины пролетов, качества напольного покрытия и др.), безопасности хранения грузов, а также с точки зрения автоматизации работы склада и компьютерной обработки его грузооборота. При редевелопменте необходимо учитывать такие современные инженерные решения как: многоярусное складирование грузов, использование гравитационных стеллажей, наклонных роликовых дорожек, оснащение зоны хранения специальными штабелирующими машинами; применение средств непрерывного транспорта с автоматической переадресацией при внутрискладском перемещении грузов. Стационарные роликовые конвейерные линии должны обеспечивать возможность перемещения груза при обслуживании складов в двух направлениях, то есть быть реверсивными. Стеллажи следует разделить на зоны по направлениям перевозок с учетом объема грузопотоков по каждому направлению. На территории логистического комплекса должна функционировать единая автоматизированная система организации и учета внутрискладского перемещения грузов.
Очевидно, что все эти мероприятия, направленные, в первую очередь, на привлечение новых арендаторов, увеличение грузооборота комплекса и, как следствие, повышение эффективности использования имеющихся площадей, связаны с привлечением новых вложений, а инвестиционный проект трансформируется в двухпериодный, который является частным случаем многопериодного потока. Для его анализа становится необходимым использование соответствующей многопериодной методологии [1].
Рассмотрим частный случай этой методологии, а именно двухгодичное и двухпериодное планирование. Как известно, с данным видом планирования связана так называемая проблема Лори и Сэвиджа (американские экономисты), которая впервые была поднята ими в 1955 году. Они на примере анализа инвестиций, направляемых в модернизацию насосной станции, показали, что проект может иметь несколько внутренних норм рентабельности, а в 1964 г. другой их коллега - американский исследователь Тейкров обосновал логику решения данной проблемы [2, 3]. Российский рынок недвижимости пока еще молод и наши девелоперы в своей массе, как нам представляется , еще не успели столкнуться с практическими примерами, определяющими необходимость интерпретации нескольких внутренних норм рентабельности при оценке эффективности проекта. Вместе с тем возникающие подобные специфические ситуации обладают, в свою очередь, известного рода неопределенностью, которая дополнительно увеличивает инвестиционные риски и может сказаться в будущем на уровне доходности проекта.
Рассмотрим практический пример двухгодичного денежного потока, определяющего редевелопмент производственной площадки в логистический терминал, который также может служить иллюстрацией двухпериодного проекта. Предположим, что существует складской комплекс, генерирующий ежегодный денежный поток в размере 1500 у.е. Если его не реконструировать (нулевой вариант), то чистый дисконтированный доход от его эксплуатации будет равен:
NPV0=1500[1+(1+E)-1+(1+E)-2] (1)
Видно, что кривая изменения NPV0(E) для 0-го варианта, показанная на рис.1, представляет монотонно убывающую функцию.
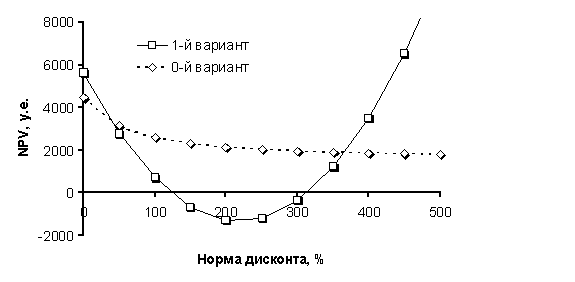
Рис.1. Графики зависимостей чистого дисконтированного потока от нормы дисконта для 0-го и 1-го вариантов двухгодичного и двухпериодного проекта.
Рассмотрим 1-й альтернативный вариант. Как и в предыдущем (нулевом) варианте, в начальный момент времени получен доход в 1500 у.е. В конце 1-го года предполагается модернизация комплекса посредством установки современного программно-аппаратного обеспечения стоимостью 9375 у.е. В результате в конце 2-го года предполагается получить доход в 13500 у.е. Следовательно, формула расчета чистого дисконтированного потока будет следующей:
NPV1=1500-9375(1+E)-1+13500(1+E)-2] (2)
Рассматривая представленный на рис.1 график этой зависимости, можно видеть, что для данного варианта имеются две внутренние нормы доходности IRR (123 и 313%) и соответственно две точки Фишера (43 и 365%).
Анализ представленных кривых показывает, что:
· для малых значений норм дисконта, расположенных левее первой точки Фишера, более эффективным является 1-й вариант;
· для больших значений норм дисконта, расположенных правее второй точки Фишера, более эффективным является также 1-й вариант;
· для средних норм дисконта, расположенных между обеими точками Фишера, эффективным является нулевой вариант;
· для норм дисконта, расположенных между двумя внутренними нормами доходности, чистый дисконтированный доход по 1-му варианту является отрицательным.
Возьмем другой пример, который условно индексируем как 2-й вариант. Допустим, что в нулевой момент времени в производственные помещения вложены средства в размере 1500 у.е. (например, осуществлена их покупка). В конце 1-го года от эксплуатации данных помещений получен доход 9750 у.е., а в конце 2-го года осуществлена повторная инвестиция средств, но в недоходный (например, в социальный) объект в размере 12000 у.е. Тогда формула расчета чистого дисконтированного дохода будет следующей:
NPV2=1500-9750(1+E)-1+12000(1+E)-2] (3)
Из представленного на рис.2 графика этой зависимости видно, что и для данного варианта имеются две внутренние нормы доходности IRR (64,5 и 397%) и две точки Фишера (126 и 351%).
Анализ представленных кривых показывает, что:
· для малых значений норм дисконта, расположенных левее первой точки Фишера, более эффективным является 0-й вариант;
· для больших значений норм дисконта, расположенных правее второй точки Фишера, более эффективным является также 0-й вариант;
· для средних значений норм дисконта, расположенных между обеими точками Фишера, эффективным является 2-ой вариант;
· для норм дисконта, расположенных между двумя внутренними нормами доходности, чистый дисконтированный доход по 1-му варианту является не только положительным, но и имеет соответствующий экстремум, а точнее максимум при Е=229%.
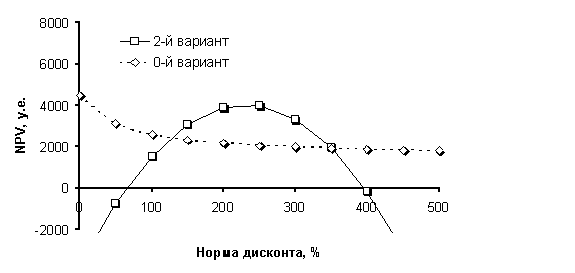
Рис.2. Графики зависимостей чистого дисконтированного потока от нормы дисконта для 0-го и 2-го вариантов двухгодичного и двухпериодного проекта.
Для обоих вариантов можно констатировать, что максимизация внутренней нормы доходности не является достаточным критерием для принятия инвестиционного решения. Очевидно, представленные специфические особенности обусловлены тем, что расчеты чистого дисконтированного дохода для 1-го и 2-го вариантов инвестиций производятся по соответствующими квадратным уравнениям. Однако, если экстраполировать данные результаты на проекты, которые разрабатываются на три и более года, то можно ожидать даже большее число внутренних норм доходности. Это связано с тем, что формулы расчета чистого дисконтированного дохода будут представлять собой полиномы, степень которых определяется числом лет принятого жизненного цикла. Следовательно, для данных полиномов в соответствии с теорией из высшей алгебры [4] при соответствующих инвестиционных параметрах может иметь место максимальное число внутренних норм доходности, определяемое числом лет оцениваемого проекта.
Разброс внутренних норм доходности не позволяет без дополнительных соглашений принять решение об инициации проекта. Например, одним из соглашений может быть следующее правило. Для снижения неопределенности необходимо оценивать рентабельность таких проектов с помощью единой минимальной нормы дисконта, рассчитываемой, исходя из принятия минимальной премии за риск. Однако в любом случае для применения предложенного соглашения или для другого альтернативного предложения априори требуется установить саму неопределенность, для чего необходимо провести адаптацию задачи нахождения корней полинома к рассмотренному инвестиционному анализу.
Резюме
В статье рассмотрены вопросы, связанные с противоречивостью некоторых критериев оценки эффективности инвестиционных проектов, включающих создание и (или) эксплуатацию объектов недвижимости. Предлагаемые выводы основаны на анализе таких критериев, как чистый дисконтированный доход и внутренняя норма доходности. На количественных примерах продемонстрировано, что оба эти критерия не являются абсолютными и в некоторых ситуациях требуется использование дополнительных соглашений, поэтому чистый дисконтированный доход и внутренняя норма доходности не могут выступать единственными критериями при оценке эффективности инвестиционных проектов.
Литература
1. Вехи экономической мысли. Теория потребительского поведения и спроса. Т.3. Под ред. В.М.Гальперина.- СПб.: Экономическая школа. 1999.
2. Three problems in rationing capital, J.H.Lorie, L.J.Savage. - Journal of Business. 1955. Vol. 28. No. 4. P. 229-239
3. Управление финансовой деятельностью предприятия. Проблемы, концепции и методы. Б.Коласс / Пер. с франц. под редакцией проф. Я.В. Соколова, - М.:Финансы, ЮНИТИ, 1997.
4. Г.Корн, Т.Корн. Справочник по математике (для научных работников и инженеров). М.: Наука, 1973. - 832 с.
|


